- Fluid mechanics and thermodynamics of two-phase flows

- Computational rheology

- Modeling of complex fluids, e.g. polymer melts and solutions, suspensions, emulsions

- Numerical simulation of viscoelastic two-phase flows

- Numerical stabilization techniques for high Weissenberg number flows

- Non-isothermal viscoelastic flows

- Robust and efficient numerical methods and algorithms for Computational Fluid Dynamics

- Error-driven adaptive remeshing and conservative field mapping on general unstructured finite volume meshes

- Software development and implementation in C++

Transient 3D simulations of rising bubbles in viscoelastic fluids

Bubbles rising in viscoelastic liquids may exhibit certain characteristic phenomena:

- a jump discontinuity of the rise velocity as a critical bubble volume is exceeded.

- a negative wake, with the liquid velocity behind the bubble pointing in a direction opposite to that in Newtonian fluids.

- a cuspidal bubble shape, with the formation of a pointed tip at the rear end of the bubble.

These characteristic features have been known for about 60 years, however it was unclear what is causing these flow phenomena.

In search for a convincing explanation, we have developed an extended volume-of-fluid (VOF) method [3,4] to study the transient rise of single bubbles in viscoelastic fluids. The validity and accuracy of the numerical method has been verified by comparing the terminal rise velocities of bubbles of different volumes. The simulation results obtained with the VOF method show quantitative agreement of the terminal rise velocities with experimental measurements. Moreover, the negative wake is observed in an almost cone-shaped region below the bubble’s trailing end. This can be seen from the visualization of the velocities in the bubble wake in Figure 1, where the negative velocities with respect to the vertical coordinate direction are represented in red color.

Results from a detailed local polymer stress and conformation tensor analysis provide new insights into the molecular orientation and stretching for the subcritical and supercritical states of the bubble motion [1]. Figure 2 shows that polymer molecules traveling along the upper bubble hemisphere are stretched in the circumferential direction, due to the flow kinematics. Depending on the relaxation time scale of the polymer, the stored elastic energy is either unloaded essentially above or below the bubble's equator. A key finding of this work is that in the subcritical state, the relaxation of the polymer molecules is completely confined to the upper half of the bubble, where the release of the stored energy slows down the bubble. In the supercritical state, the molecular relaxation essentially takes place in the lower half of the bubble, inducing an upwards-directed force that accelerates the bubble. Moreover, this relaxation of the hoop-stress in the lower bubble hemisphere gives rise to a self-amplification of the effect and thus causing the bubble rise velocity to jump to a higher level.

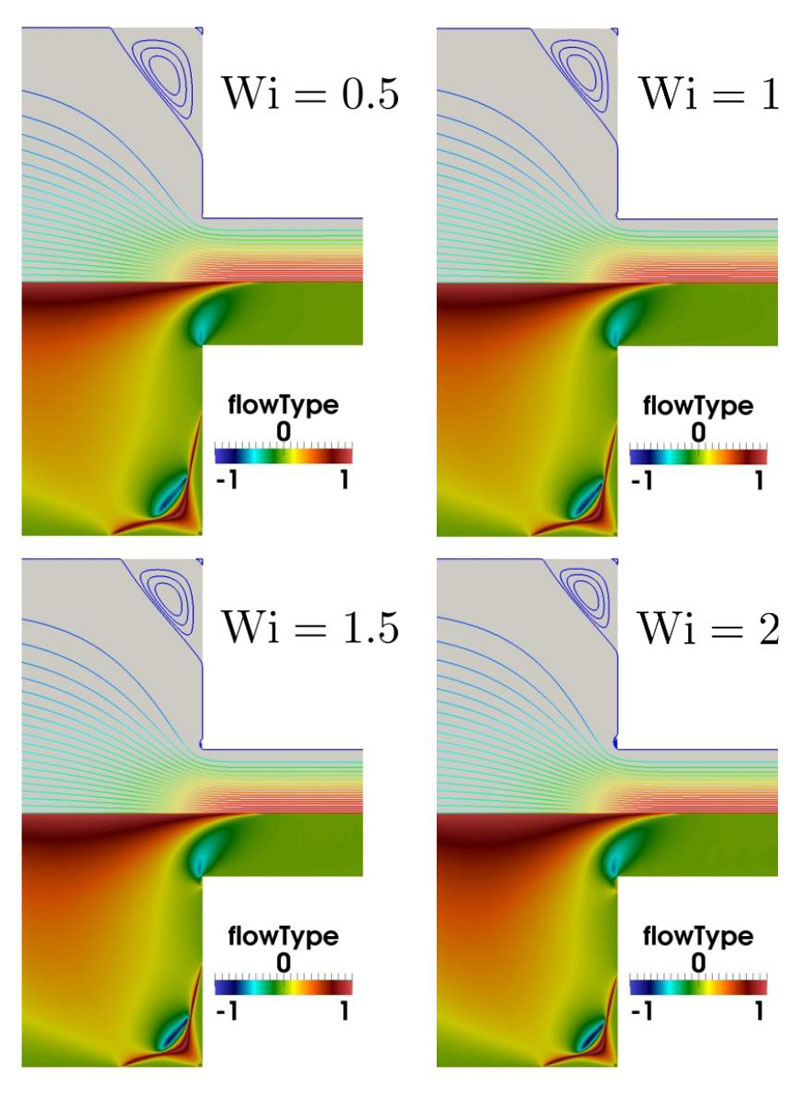
Computational rheology at high Weissenberg numbers

The “High Weissenberg Number Problem’’ (HWNP) has been a major challenge in computational rheology for the past three decades. It refers to the loss of convergence of all numerical methods beyond some limiting value of the fluid elasticity, quantified by a critical Weissenberg number. The critical value varies with the problem, in particular with regard to the flow geometry and the fluid constitutive model. Although a complete solution is not known until today, several effective numerical stabilization methods have been developed to cope with the HWNP. However, there is a multitude of constitutive models describing viscoelastic material behavior, with which the stabilization approaches are to be combined. For the first time, this combination has been realized in a general way by deriving model-independent forms of the stabilized equations. We have developed a generic numerical framework that provides full combinatorial flexibility between a wide range of rheological models for viscoelastic polymer melts and solutions on the one hand, and cutting-edge stabilization methods on the other hand. The framework has been implemented into a new comprehensive and flexible C++ library which is built on top of the open-source library OpenFOAM. Our methods have been validated in several computational benchmark problems over a large range of Weissenberg numbers [5,6].

Links

ORCID

Google scholar

LinkedIn

ResearchGate

Publications

[1] Bothe, D., Niethammer, M., Pilz, C. and Brenn, G.: On the molecular mechanism behind the bubble rise velocity jump discontinuity in viscoelastic liquids. J. Non-Newton. Fluid Mech. 302, (2022), 104748. DOI

[2] Meburger, S., Niethammer, M., Bothe, D. and Schäfer, M.: Numerical simulation of non-isothermal viscoelastic flow at high Weissenberg numbers using a finite volume method on general unstructured meshes. J. Non-Newton. Fluid Mech. 287, (2021), 104451. DOI

[3] Niethammer, M.: A Finite Volume Framework for Viscoelastic Flows at High Weissenberg Number. Dissertation, Technische Universität Darmstadt, 2019. ISBN: 9783843940641.

[4] Niethammer, M., Brenn, G., Marschall, H. and Bothe, D.: An Extended Volume of Fluid Method and its Application to Single Bubbles Rising in a Viscoelastic Liquid. J. Comput. Phys. 387 (2019), 326-355. DOI

[5] Niethammer, M., Marschall, H. and Bothe, D.: Robust Direct Numerical Simulation of Viscoelastic Flows. Chemie Ing. Tech. 91, 4 (2019), 522-528. DOI

[6] Niethammer, M., Marschall, H., Kunkelmann, C. and Bothe, D.: A numerical stabilization framework for viscoelastic fluid flow using the finite volume method on general unstructured meshes. Int. J. Numer. Methods Fluids 86, 2 (2018), 131-166,. DOI